Von Dipl.-Phys. Dr. Jan Olzem
Im ersten Teil des Artikels haben wir uns ausführlich mit der Zeitreihe der Jahresmitteltemperaturen in Deutschland auseinandergesetzt und die Frage aufgeworfen, welchen Einfluß das Wachstum der Städte auf die gemessene Temperaturentwicklung der letzten Jahrzehnte gehabt hat. Um dies zu klären, muss ein geeignetes Kriterium gefunden werden, mit dessen Hilfe sich die unmittelbare Umgebung einer Wetterstation als ländlich bzw. urban (städtisch) charakterisieren lässt. Auf diese Weise können urban gelegene Stationen separat betrachtet und Unterschiede in der Temperaturentwicklung gegenüber der ländlichen Umgebung dargestellt werden.
In den letzten Jahren hat sich ein sehr nützliches Mittel für diesen Zweck herauskristallisiert: die satellitengestützte Kartierung der nächtlichen Lichtintensität (Nighttime Lights) aus künstlichen Quellen. Der Zusammenhang leuchtet unmittelbar ein: Straßenlaternen, Gebäudebeleuchtung, Fahrzeugscheinwerfer, Leuchtreklame und viele andere anthropogene Lichtquellen sind typische Merkmale der städtischen Umgebung und eng mit den Ursachen des städtischen Wärmeinseleffektes (Bebauung und Versiegelung) verknüpft. Hinzu kommt die weiträumige atmosphärische Streuung des Lichtes in der Umgebung der Städte. Tatsächlich ist der Zusammenhang zwischen Urbanisierung und Lichtintensität seit einigen Jahren intensiv erforscht und sehr gut belegt worden. Es bietet sich also an, die Lichtintensität in der Umgebung einer Wetterstation als Maß für den Wärmeinseleinfluß zu nutzen.
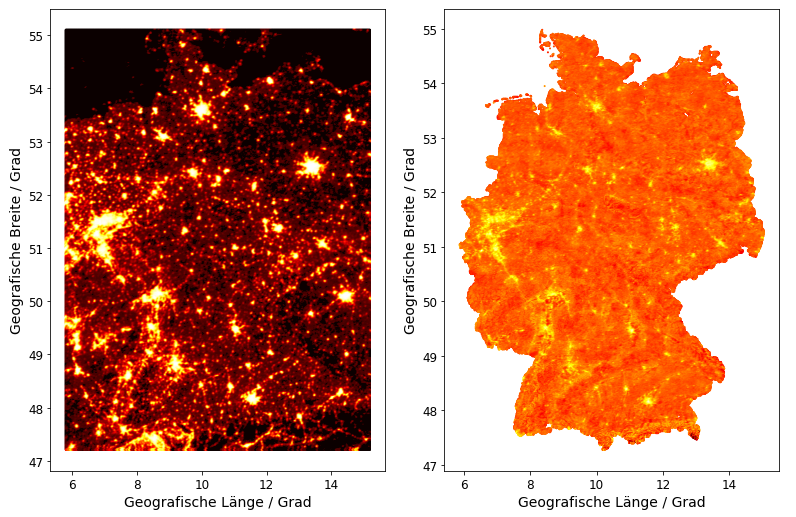
Abbildung 6: Links: die Verteilung der Lichtintensität aus künstlichen Lichtquellen (Nighttime Lights) in Deutschland (Datenquelle: NOAA, US Air Force Weather Agency); rechts: die Verteilung der AHI (Datenquelle: Benz et al. 2017)
Satellitendaten zur nächtlichen Lichtintensität sind aus verschiedenen Quellen frei verfügbar. Die linke Seite der Abbildung 6 zeigt die Messung des OLS-Instrumentes an Bord eines DMSP-Satelliten (US-Verteidigungsministerium) für das Jahr 2013. Es handelt sich um ein Komposit aus vielen über das Jahr verteilten Einzelmessungen, wobei temporäre Lichtquellen (z.B. Wolken, Brände) herausgefiltert wurden. Die Lichtintensität wird in der abstrakten Einheit DN angegeben und reicht von 1 (stockfinster) bis 63 (sehr hell). Die Daten liegen in Form eines Rasters mit einer Auflösung von 30 Bogensekunden vor, das entspricht etwas weniger als 1 Kilometer auf der Erdoberfläche. Auf diese Weise kann jedem Ort in Deutschland ein DN-Wert für die Lichtintensität direkt zugeordnet werden.
Abbildung 7: Wetterstationen mit DN >= 15 (urban, rote Punkte) und DN < 15 (ländlich, blaue Punkte) in der Mainregion vor dem Hintergrund der Nighttime Lights
Somit haben wir nun ein Maß für die Charakterisierung der Umgebung von Wetterstationen zur Hand. Abbildung 7 zeigt dies beispielhaft für die Mainregion vor dem Hintergrund der Nighttime Lights. Jeder farbige Punkt stellt den Ort einer der betrachteten Wetterstationen in der Region dar, wobei zwischen ländlich (blau) und urban (rot) unterschieden wird. Als Grenzwert wurde hier DN = 15 gewählt, was einen etwas willkürlichen aber in der Literatur durchaus gängigen Wert darstellt. Zusätzlich ist die Lage einiger größerer Städte eingezeichnet. Ein erheblicher Teil der Stationen befindet sich demnach tatsächlich in stark bebauten Gebieten (bzw. “befand”, da nicht alle Stationen heute noch in Betrieb sind).
Abbildung 8: Zehnjährige gleitende Mittelwerte der Jahresmitteltemperatur (unkorrigierte Rohdaten) in Deutschland seit dem Jahr 1900 für verschiedene DN-Obergrenzen. Die Mittelwerte sind zentriert und werden somit erst ab dem Jahr 1905 dargestellt.
Nun wird es interessant. Wie sieht der Temperaturverlauf der letzten Jahrzehnte in Abhängigkeit von der Lage der Wetterstationen aus? In Abbildung 8 ist die Temperaturentwicklung für verschiedene Obergrenzen von DN dargestellt, d.h. beginnend mit den Stationen in den nachtdunkelsten Gebieten (rosa) bis hin zu allen betrachteten Stationen (grau). Zur Glättung der Kurven wurde ein zehnjähriger gleitender Mittelwert verwendet. Zunächst einmal ist deutlich erkennbar, dass die Temperatur tatsächlich mit der nächtlichen Lichtintensität variiert – je dunkler die Umgebung, desto niedriger ist auch die mittlere Temperatur. Bei genauem Hinsehen offenbart sich allerdings eine faustdicke Überraschung: in den nachtdunkleren Gebieten mit niedrigem DN ist die Temperatur offensichtlich sehr viel stärker angestiegen als im Mittel aller Stationen (einschließlich der Städte). Die Differenz von über 2°C ist erheblich und stellt genau das Gegenteil dessen dar, was man vom Wärmeinseleffekt erwarten würde. Wie kann das sein?
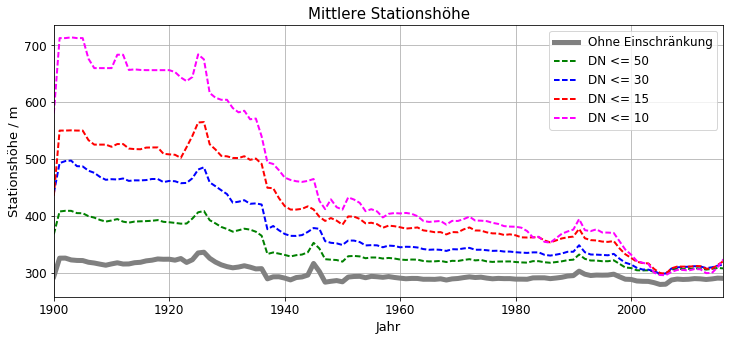
Abbildung 9: Änderung der mittleren Stationshöhe für verschiedene Werte von DN
Die Lösung des Rätsels hat wieder einmal etwas mit der Höhe über N.N. zu tun. Betrachtet man die Veränderung der gemittelten Stationshöhe für die verschiedenen DN-Obergrenzen (Abbildung 9), zeigt sich ein klarer Trend. Während die über alle Stationen gemittelte Höhe (grau) mit der Zeit nur geringfügig abgenommen hat, liegen die nachtdunkelsten Stationen (rosa) heute im Durchschnitt mehr als 350 m tiefer als zu Beginn des letzten Jahrhunderts. Dies läßt sich folgendermaßen interpretieren: Stationen in Höhenlagen wurden aufgegeben und zum Teil durch neue Messstellen an vergleichbar entlegenen, jedoch weniger gebirgigen Orten, ersetzt. Sicherlich spielen die Unterhaltskosten dabei eine wichtige Rolle. Hier zeichnen sich erste Hinweise ab auf ein Tendenz, von der später noch ausführlich die Rede sein wird.
Abbildung 8 zeigt also einen Effekt, der hauptsächlich auf der Veränderung des Messnetzes beruht, da die nächtliche Lichtintensität eben auch eine starke Korrelation zur Höhe aufweist. Eine Möglichkeit, dies in den Griff zu bekommen, bestünde nun darin, die Temperaturdaten mit Hilfe der im ersten Teil dieses Artikels beschriebenen Höhenkorrektur einheitlich auf N.N. zu reduzieren, d.h. den Einfluß der Höhe auf die Temperatur herauszurechnen. Die Sache hat aber leider einen Haken: die Höhenkorrektur ist aus verschiedenen Gründen nicht perfekt und kann somit den Höheneinfluß nicht immer restlos eliminieren. Da der Höheneffekt sehr ausgeprägt ist, bestünde nach der Korrektur das Risiko von Restabhängigkeiten, die in den Daten verbleiben und nur sehr schwer von einem möglichen echten Wärmeinselsignal zu trennen sind.
Besser wäre, wenn man DN ersetzen könnte durch eine Größe, die per se weniger anfällig für derartige Störeffekte ist. Ein solcher Ansatz wurde 2017 von Forschern des KIT (Karlsruhe) und der TH Ingolstadt (Benz et al.) publiziert. Im kaltesonne-Blog wurde darüber berichtet. Die Autoren definieren dort die Größe AHI (anthropogenic heat intensity), die die Temperaturdifferenz eines Ortes gegenüber seinem ländlich geprägten Umland darstellt. Als Quelle der Temperaturmesswerte dienten auch hier die Wetterstationen des DWD. Ein Ort in der Umgebung wird von den Autoren als ländlich eingestuft, wenn die nächtliche Lichtintensität dort gering ist (DN < 15). Es handelt sich bei AHI also im Prinzip um einen Indikator, der direkt gemessene Temperaturdifferenzen widergibt, aber indirekt dennoch auf den Nighttime Lights basiert. Frau Benz hat freundlicherweise die AHI-Daten für diese Analyse zur Verfügung gestellt.
Wie die Nighttime Lights kann auch AHI flächendeckend für jeden Ort in Deutschland bestimmt werden. Eine Karte der AHI-Werte zeigt die rechte Seite der Abbildung 6 am Anfang des Artikels: Ihre Verteilung ähnelt sehr stark derjenigen der Nighttime Lights, was nicht verwunderlich ist, da AHI ja auf Basis der nächtlichen Lichtintensität berechnet wird. Der Vorteil von AHI besteht jedoch darin, dass die Temperatur an einem Ort direkt zu seiner unmittelbaren Umgebung in Bezug gesetzt wird. Ersetzt beispielsweise eine neue Wetterstation eine kürzlich geschlossene, so “wandert” die Bezugsregion sozusagen mit, was den störenden Einfluss von Größen wie etwa der Höhe wirkungsvoll unterdrückt.
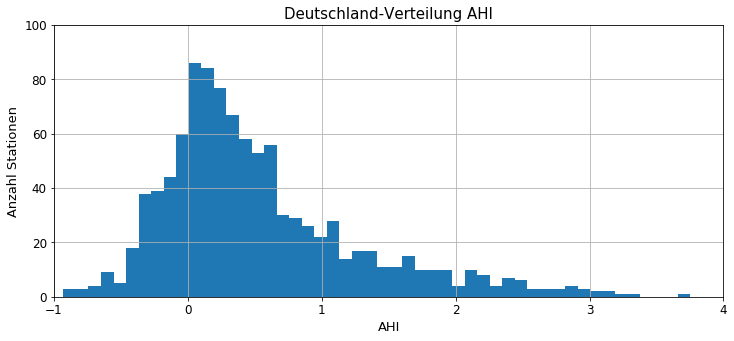
Abbildung 10: Häufigkeitsverteilung der Stationen nach AHI-Wert (Datenquelle: Benz et al. 2017)
Die Häufigkeitsverteilung der AHI-Werte der DWD-Wetterstationen zeigt Abbildung 10. AHI liegt zwischen -1°C und ca. +3,5°C, d.h. die stärksten Wärmeinseln sind demnach im Mittel über 3°C wärmer als ihre Umgebung (z.B. die Stationen München-Bogenhausen, Dresden-Mitte, Hamburg-Deutsche Seewarte, Augsburg-Sankt Stephan, Berlin-Invalidenstraße, Berlin-Ostkreuz und Berlin-Mitte). Die Spitzenwerte der Temperaturdifferenz zum Umland können an einzelnen Tagen jedoch auch deutlich darüber liegen. Damit ist bereits allein aufgrund der Verteilung der AHI-Werte klar, dass der Wärmeinseleffekt existiert und in den DWD-Daten messbar ist.
Benz et al. lassen bei der Auswahl der ländlichen Umgebung eines Ortes Höhenunterschiede von bis zu ±90 m zu. Auf diese Weise ist es durchaus möglich, dass die ländliche Umgebung eines Ortes im Mittel höher liegt und dadurch etwas kühler ist als der Ort selbst, so dass ihm ein AHI-Wert unter null zugeordnet wird. Darüberhinaus gibt es natürlich auch weitere Faktoren, die die mittlere Temperatur lokal beeinflussen können. Beispiele für Orte mit sehr niedrigem AHI-Wert (ca. -0,9°C) sind: Zwieselberg (Allgäu), Schulenberg (Oberharz), Veilsdorf (Thüringer Wald) und Mittenwald-Buckelwiesen (Oberbayern), die sich alle in Gegenden mit vergleichsweise hoher Reliefenergie befinden.
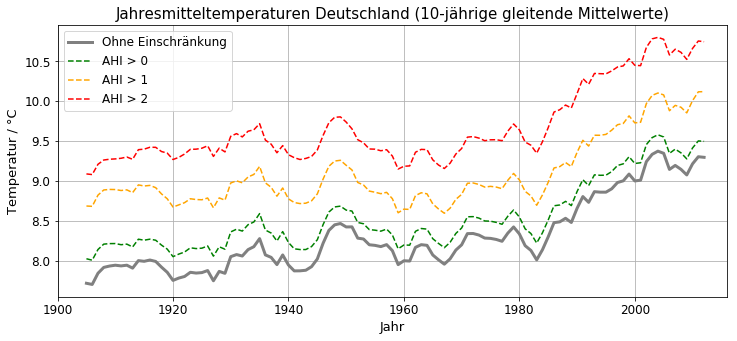
Abbildung 11: Zehnjährige gleitende Mittelwerte der Jahresmitteltemperatur (unkorrigierte Rohdaten) Deutschland für verschiedene AHI-Obergrenzen
Abbildung 11 zeigt die Temperaturentwicklung für verschiedene Obergrenzen von AHI. Die rote Kurve gibt den Temperaturverlauf für die Wetterstationen mit den höchsten Temperaturdifferenzen gegenüber ihrer ländlichen Umgebung wieder (AHI > 2), die graue Kurve diejenige für alle Wetterstationen. Es ist ein deutlicher Temperaturunterschied erkennbar, wie es aufgrund der Häufigkeitsverteilung der AHI (Abbildung 10) zu erwarten war. Im Gegensatz zu den Temperaturverläufen für verschiedene DN (Abbildung 8) fehlt jedoch der durch die Verschiebung hin zu geringerer Stationshöhe verursachte starke Temperaturanstieg in ländlichen Gebieten mit niedrigen AHI-Werten. Offensichtlich haben wir nun tatsächlich einen zuverlässigen Wärmeinselindikator bei der Hand, der nur in geringem Maße von der Entwicklung des DWD-Messnetzes beeinflusst wird.
Die entscheidende Frage ist nun, ob – und ggf. wie stark – der Wärmeinseleffekt zum Anstieg der Temperaturen in Deutschland in den letzten Jahrzehnten beigetragen hat. Anders ausgedrückt: Stieg die Temperatur in den Städten schneller als auf dem Land? Mit dieser Frage werde ich mich im dritten Teil des Artikels befassen.